Combinatorial Laplacians on Acyclic Complexes

국웅 교수 (서울대학교)
2013. 10. 10.

The main topic of the talk is a determinantal formula for high dimensional tree numbers of acyclic complexes via combinatorial Laplace operators 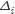. This result is a generalization of Temperley's tree number formula for graphs, motivated by a simple (but not well-known) observation that Temperley's method uses combinatorial Laplacian 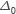in dimension zero. 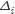The talk will begin with a brief survey of properties and applications of including network theory and topological data analysis. Towards the end, we will discuss a logarithmic version of the main formula of the talk and demonstrate intriguing applications of its generating function to various complexes that arise naturally in combinatorics.