A New Approach to Discrete Logarithm with Auxiliary Inputs

천정희 (서울대학교)
2013. 02. 19.

Let 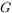be a cyclic group with generator . The discrete logarithm problem with auxiliary inputs (DLPwAI) is asked to find 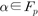with auxiliary inputs , ,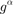…, 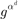. In Eurocrypt 2006, an algorithm is proposed to solve DLPwAI i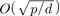n when 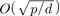. In this paper, we reduce the DLPwAI to the problems to find polynomials with small value sets or to find efficiently.
In this talk, we propose a new approach to solve DLPwAI concentrating on the behavior of function mapping between the finite fields rather than using an embedding to auxiliary groups. This result shows the relation between the complexity of the algorithm and the number of absolutely irreducible factors of the substitution polynomials, hence enlightens the research on the substitution polynomials.
More precisely, with a polynomial 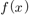of degree over 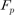, the proposed algorithm shows the complexity 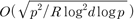group operations to recover with , , 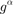, 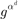where 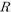denotes the number of pairs 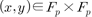such that 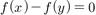. As an example using the Dickson polynomial, we reveal 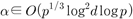group operations when .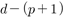